
A fractal is a complex geometric pattern that can be subdivided in parts, each of which is (at least approximately) a smaller copy of the whole. Fractals are generally "self-similar" (the bits look like the whole) and independent of scale (they look similar, no matter how close you zoom in). Benoit Mandelbrot, the discoverer of the Mandelbrot set, coined the term "fractal" in 1975 from the Latin fractus meaning "to break". Because fractals are generally made of irregular curves or shapes repeated at every scale they are difficult to represent with classical geometry, and have developed into their own branch of mathematics.

Many mathematical structures are fractals; e.g. the Sierpinski triangle, Koch snowflake, Peano curve, Mandelbrot set and Lorenz attractor. Fractals also describe many real-world objects that do not have simple geometric shapes, such as clouds, mountains, turbulence, and coastlines. Fractal type equations are also used to as the generative engines behind many "artifical life" simulations. As an example of a simple fractal, consider the following set of instructions:
Set three points (A, B and C). Start somewhere in between the three points. Randomly select one of the three points (say B). Move halfway between wherever you are and that point and leave a dot. Then randomly select one of the three points again (maybe A this time). Move halfway between your current position and that point and leave another dot. Repeat this process again and again many times.
What pattern do you think will emerge?
The following graphic was created by a computer program applying the above instructions (known as the Sierpinski triangle):
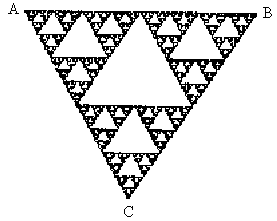
From an NLP perspective, fractals are a good example of how a simple process at the level of deep structure can generate a complex pattern at the level of surface structure. The sophistication and complexity of the resulting surface structure belies the simplicity of the deeper structure pattern which generates it.
Being able to identify the underlying pattern (deep structure) which generates a fractal is a good illustration of what is known as "code congruence" in modeling. The goal of modeling is to make descriptions of some behavior or phenomenon that will allow us to reproduce it, or some aspect of it. One of the problems that people encounter in attempting to model the behavior of others is that they become overwhelmed by the complexity of the resulting patterns. Modeling the deeper structure behind behaviors involves identifying the generative beliefs and strategies which underlie our overt actions. Relatively simple cognitive processes (analogous to the instructions which produce the Sierpinski triangle) often produce complex behaviors. Bandler and Grinder's Meta Model is a good example of this. It is a type of "linguistic fractal." By identifying a basic set of linguistic distinctions and responding with simple questions, a person can produce a sophisticated verbal interaction similar to that of an experienced therapist.
Descriptions of generative processes are typically more "code congruent" than descriptions of the resulting content. As an analogy, the attempt to describe the resulting pattern of the Sierpinski triangle in terms of objects_ i.e., "big triangles and little triangles"_ would require a great deal of information if one were to attempt to reproduce the pattern precisely. The sizes and locations of many different "objects" would need to be specified. The simple instructions used to actually create the fractal, however, do not operate at all in terms of specifying "locations and sizes of triangles." Rather, they operate on the basis of identifying reference points (A, B and C) and relationships with respect to those points (moving "half way" between a current location and a chosen point).
It should be pointed out, by the way, that applying the Sierpinski triangle instructions to other numbers of reference points does not produce the same results. If four points are used instead of three, for instance, no coherent pattern emerges. Instead of "big squares and little squares" the result appears to be just a random placement of dots. If five reference points are used, a pattern again results (that looks somewhat like a "sand dollar"), but which is nothing like the sophisticated triangular pattern which emerges from using three reference points.

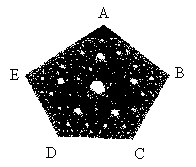
This reflects another difficulty people face when modeling. Patterns that produce the desired results in one set of circumstances, do not produce the same effects when the context or conditions change. A pattern or rule that works effectively to produce order among a group of three people, for example, may produce only random results if a fourth person is added. A creativity strategy that works well to integrate three materials or ideas may falter if a fourth item is included. While this is not always obvious when working with human behavior, it becomes graphically clear when attempting to produce fractals.
Thus, a better understanding of fractals can teach us many practical things about modeling human behaviors. Many behaviors could be considered to be types of "neurolinguistic" fractals. Dance, for instance is a type of somatic fractal. Many forms of music are a type of auditory fractal (consider Ravel's Bollero, or Pacelbel's Canon in D, for example). Clearly, many types of images are created as a result of the intuitive application of fractal patterns.
For information on Robert Dilts’ products and services, please see Upcoming Seminars or Robert’s Product Page or return to Home Page. If you have problems or comments concerning our WWW service, please send e-mail to the following address: michaelp@bowsprit.com.
This page, and all contents, are Copyright © 1998 by Robert Dilts., Santa Cruz, CA.